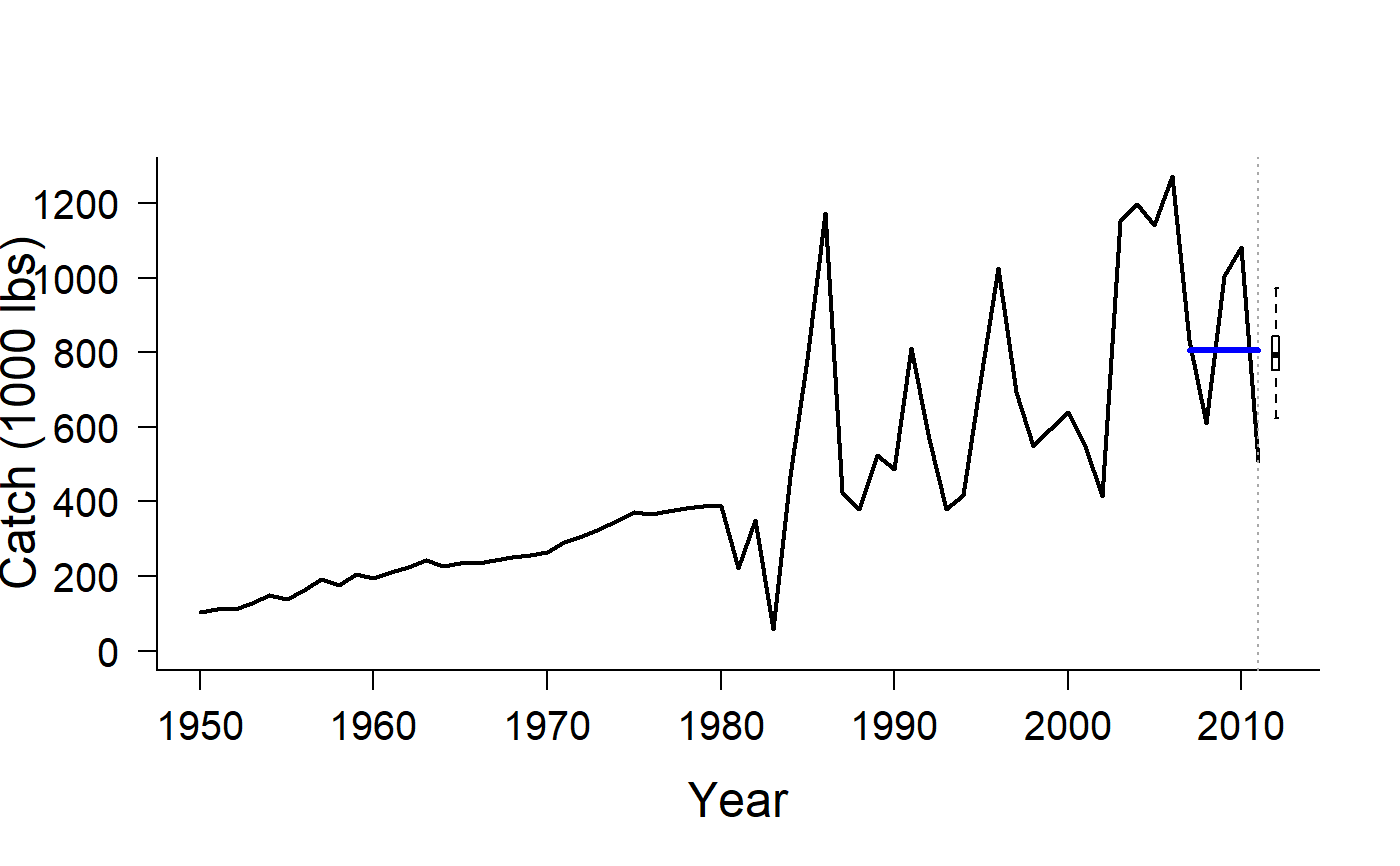
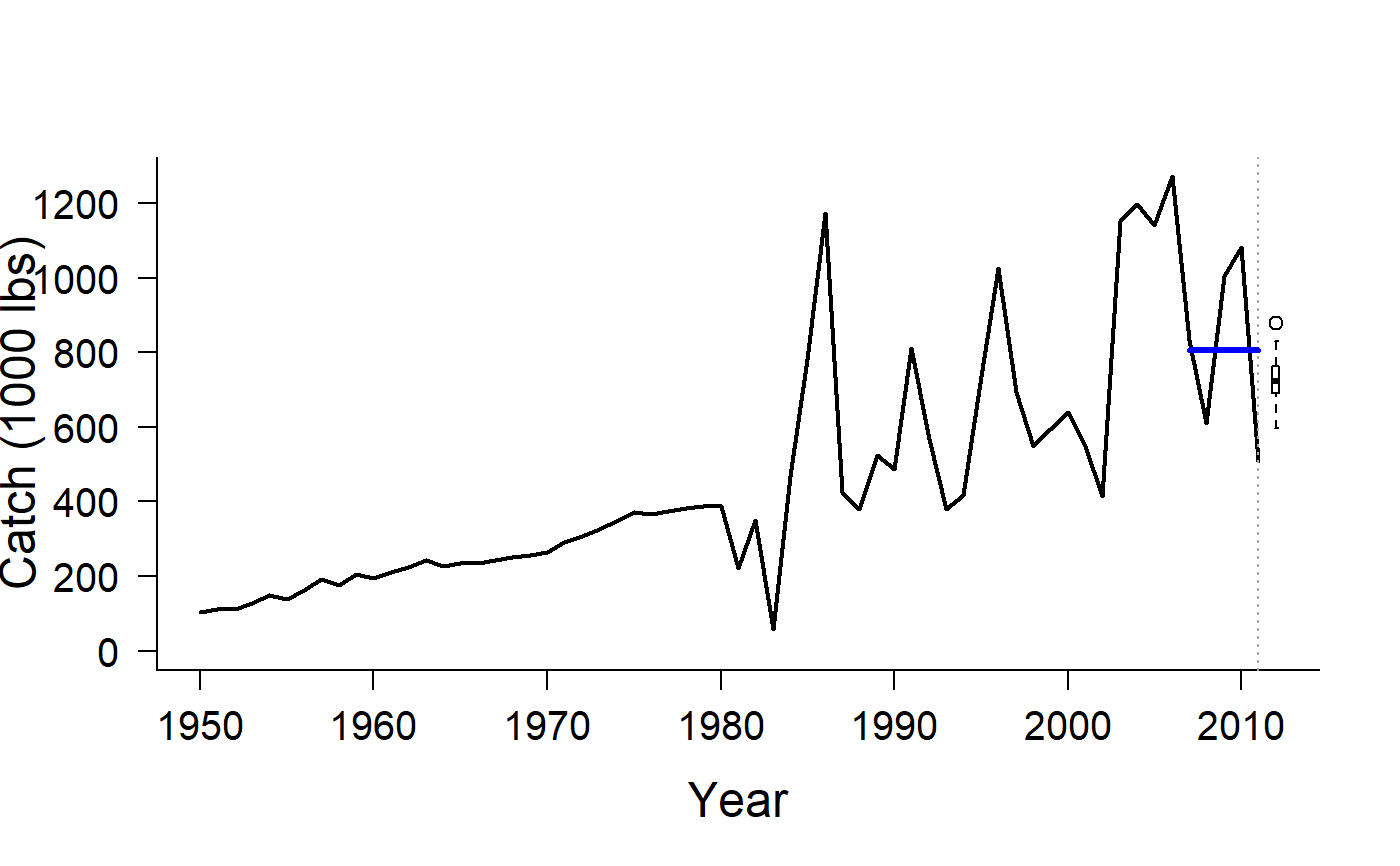
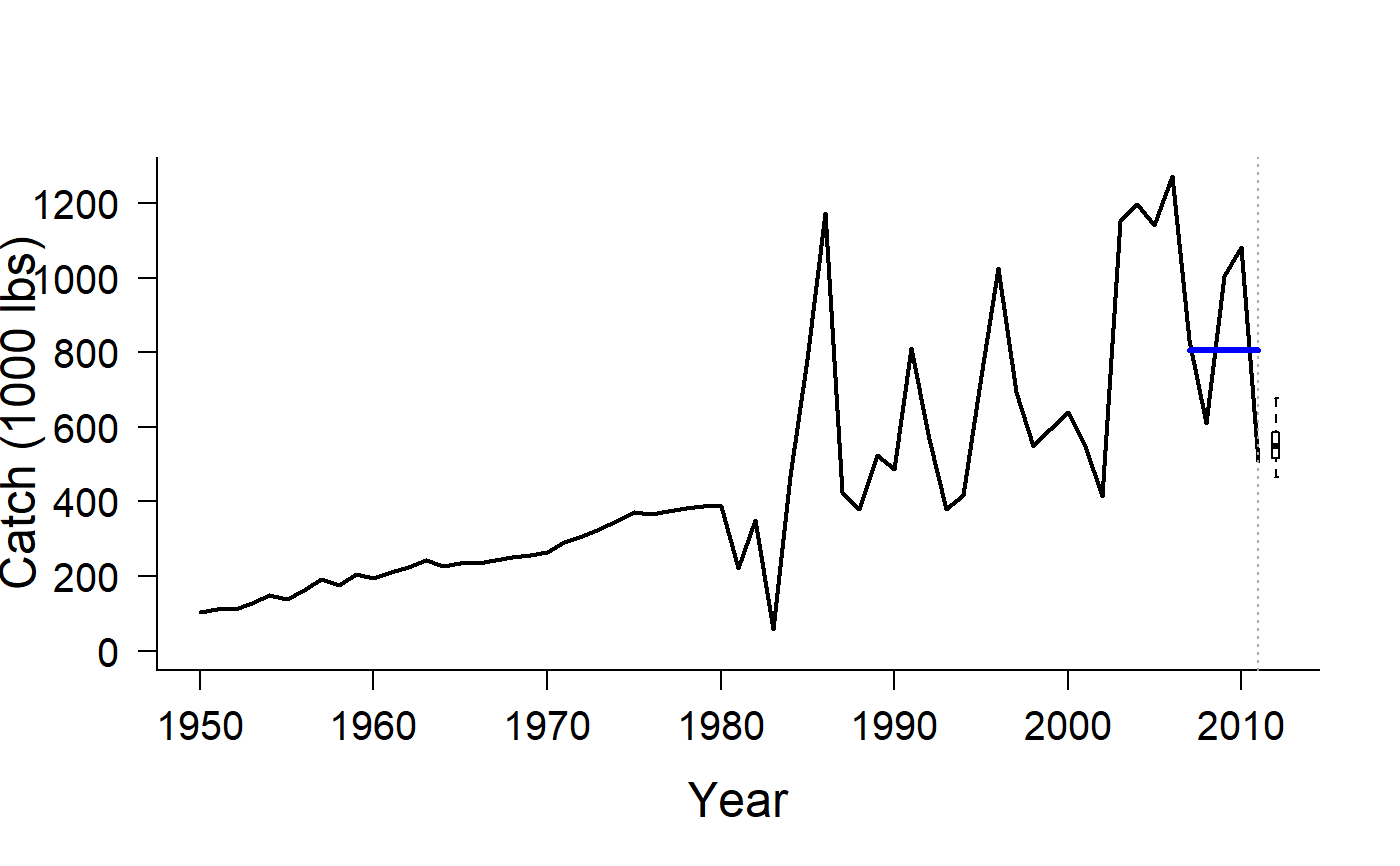
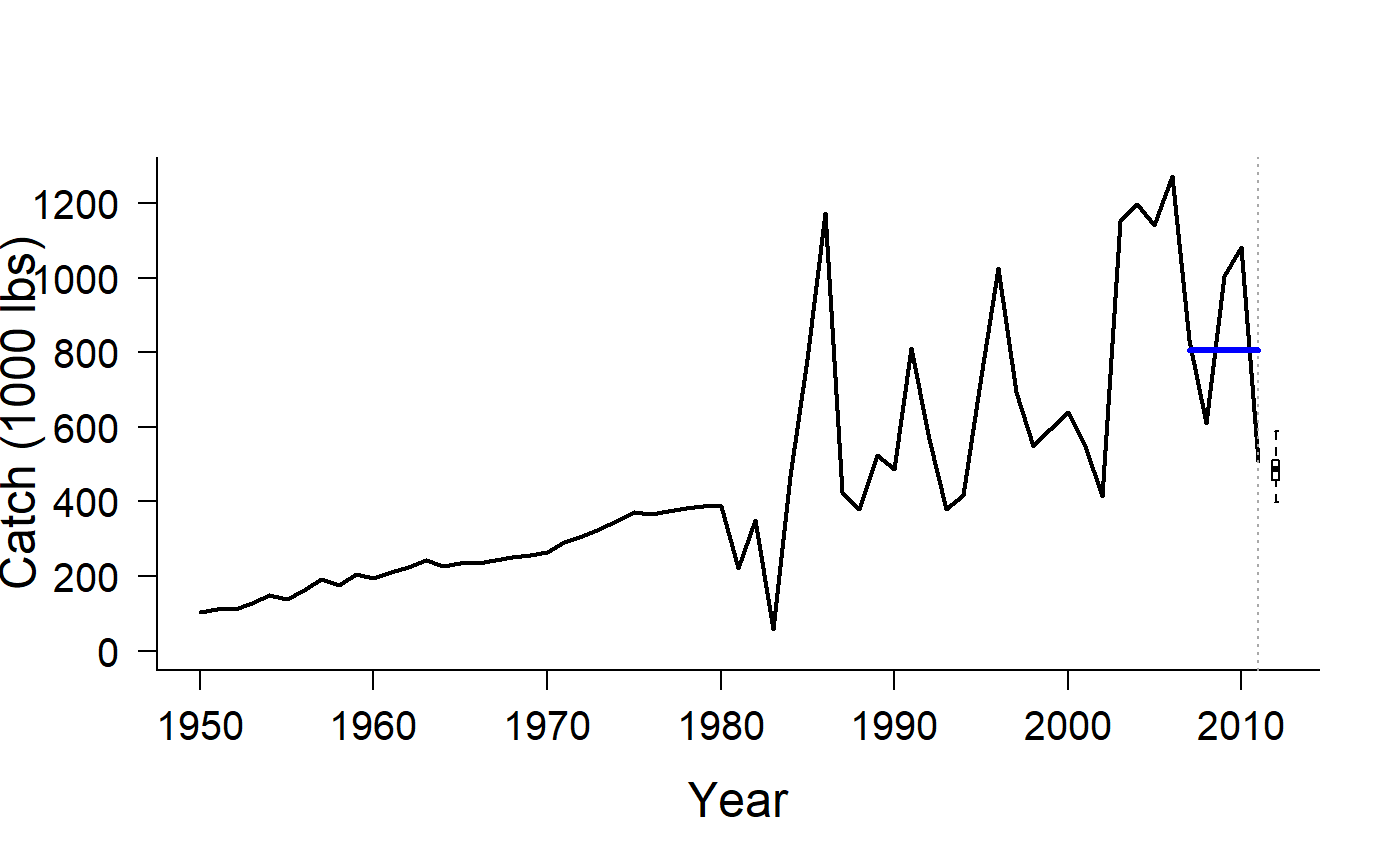
Geromont and Butterworth (2015) Constant Catch

The TAC is the average historical catch over the last yrsmth (default 5) years, multiplied by (1-xx)

CC1(x, Data, reps = 100, plot = FALSE, yrsmth = 5, xx = 0)

CC2(x, Data, reps = 100, plot = FALSE, yrsmth = 5, xx = 0.1)

CC3(x, Data, reps = 100, plot = FALSE, yrsmth = 5, xx = 0.2)

CC4(x, Data, reps = 100, plot = FALSE, yrsmth = 5, xx = 0.3)

CC5(x, Data, reps = 100, plot = FALSE, yrsmth = 5, xx = 0.4)

CurC(x, Data, reps = 100, plot = FALSE, yrsmth = 1, xx = 0)

Arguments

x

A position in the data object
Data

A data object
reps

The number of stochastic samples of the MP recommendation(s)
plot

Logical. Show the plot?
yrsmth

Years over which to calculate mean catches
xx

Parameter controlling the TAC. Mean catches are multiplied by (1-xx)

Value

An object of class Rec with the TAC slot populated with a numeric vector of length reps

Details

The TAC is calculated as: $$\textrm{TAC} = (1-x)C_{\textrm{ave}}$$ where x lies between 0 and 1, and \(C_{\textrm{ave}}\) is average historical catch over the previous yrsmth years.

The TAC is constant for all future projections.

Functions

  • CC1: TAC is average historical catch from recent yrsmth years

  • CC2: TAC is average historical catch from recent yrsmth years reduced by 10\

  • CC3: TAC is average historical catch from recent yrsmth years reduced by 20\

  • CC4: TAC is average historical catch from recent yrsmth years reduced by 30\

  • CC5: TAC is average historical catch from recent yrsmth years reduced by 40\

  • CurC: TAC is fixed at last historical catch

Required Data

See Data for information on the Data object

CC1: Cat, LHYear, Year

Rendered Equations

See Online Documentation for correctly rendered equations

References

Geromont, H. F., and D. S. Butterworth. 2015. Generic Management Procedures for Data-Poor Fisheries: Forecasting with Few Data. ICES Journal of Marine Science: Journal Du Conseil 72 (1). 251-61.

See also

Other Constant Catch MPs: GB_CC()

Examples

CC1(1, DLMtool::Cobia, plot=TRUE)
#> TAC (median) 
#>     793.0111 

CC2(1, DLMtool::Cobia, plot=TRUE)
#> TAC (median) 
#>     721.9369 

CC3(1, DLMtool::Cobia, plot=TRUE)
#> TAC (median) 
#>      640.544 

CC4(1, DLMtool::Cobia, plot=TRUE)
#> TAC (median) 
#>     548.6459 

CC5(1, DLMtool::Cobia, plot=TRUE)
#> TAC (median) 
#>     485.7275 

CurC(1, DLMtool::Cobia, plot=TRUE)
#> TAC (median) 
#>      491.539