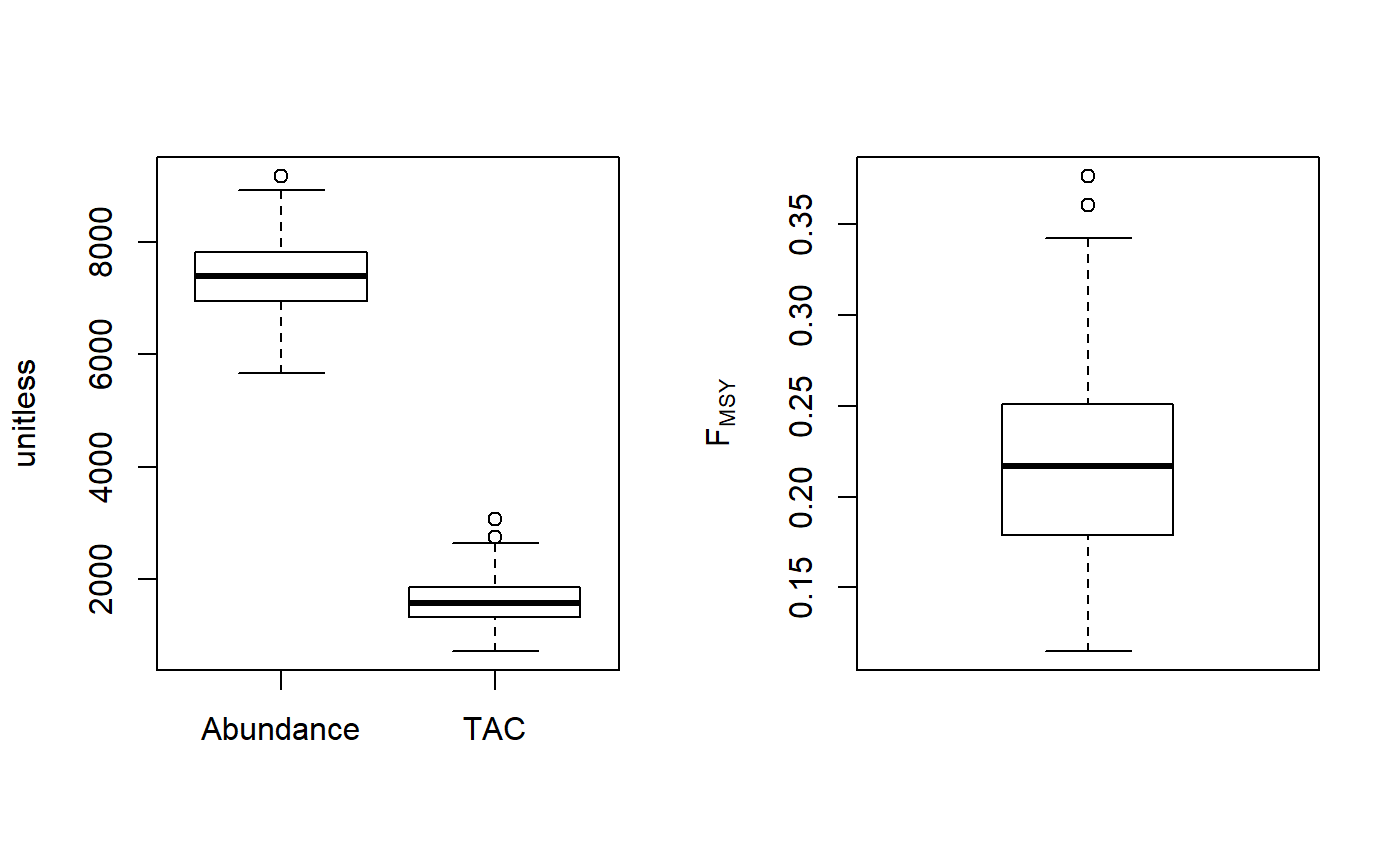
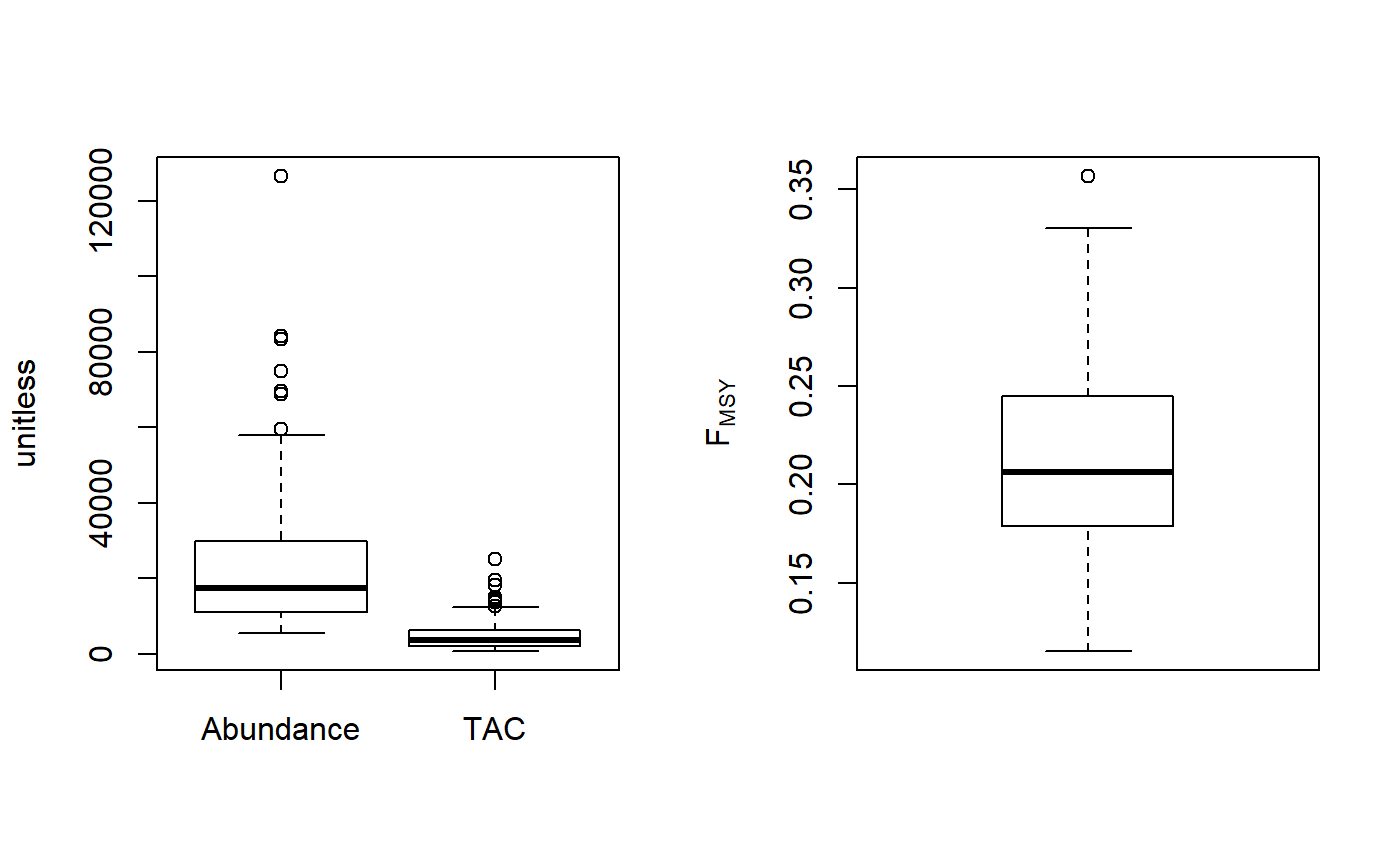
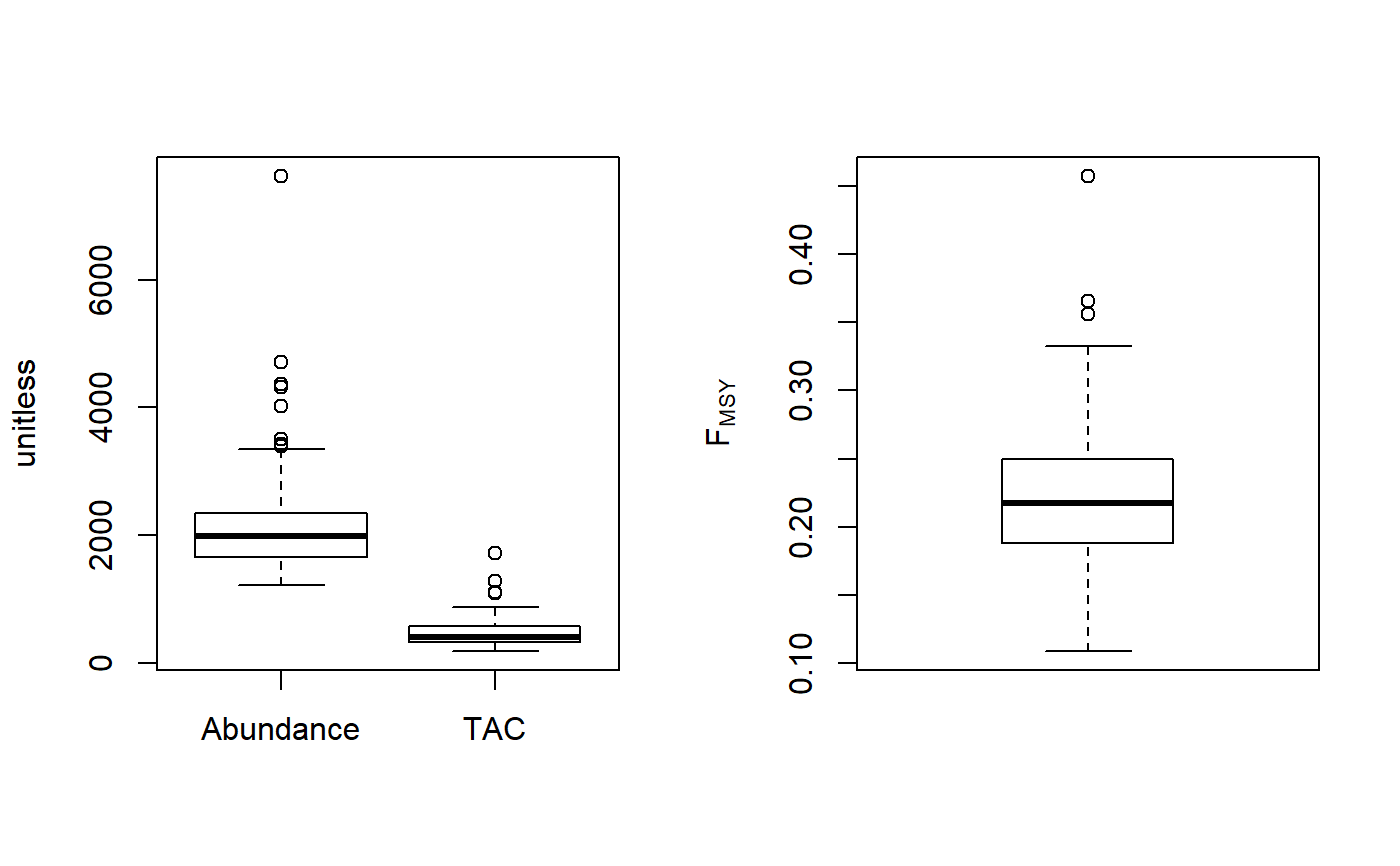
Demographic FMSY method

FMSY is calculated as r/2 where r is calculated from a demographic approach (inc steepness). Coupled with an estimate of current abundance that gives you the OFL.

Fdem(x, Data, reps = 100, plot = FALSE)

Fdem_CC(x, Data, reps = 100, plot = FALSE, Fmin = 0.005)

Fdem_ML(x, Data, reps = 100, plot = FALSE, Fmin = 0.005)

Arguments

x

A position in the data object
Data

A data object
reps

The number of stochastic samples of the MP recommendation(s)
plot

Logical. Show the plot?
Fmin

The minimum fishing mortality rate derived from the catch-curve analysis

Value

An object of class Rec with the TAC slot populated with a numeric vector of length reps

Details

The TAC is calculated as: $$\textrm{TAC} = F_{\textrm{MSY}} A$$ where A is an estimate of current abundance, and \(F_{\textrm{MSY}}\) is estimated as \(r/2\), where \(r\) is the intrinsic rate of population growth, estimated from the life-history parameters using the methods of McAllister et al. (2001).

Functions

  • Fdem: Current abundance is assumed to be known (i.e Data@Abun)

  • Fdem_CC: Current abundance is estimated from catch curve analysis

  • Fdem_ML: Current abundance is estimated from mean length

Required Data

See Data for information on the Data object

Fdem: Abun, FMSY_M, L50, MaxAge, Mort, steep, vbK, vbLinf, vbt0, wla, wlb

Fdem_CC: CAA, Cat, FMSY_M, L50, MaxAge, Mort, steep, vbK, vbLinf, vbt0, wla, wlb

Fdem_ML: CAL, Cat, FMSY_M, L50, Lbar, Lc, MaxAge, Mort, steep, vbK, vbLinf, vbt0, wla, wlb

Rendered Equations

See Online Documentation for correctly rendered equations

References

McAllister, M.K., Pikitch, E.K., and Babcock, E.A. 2001. Using demographic methods to construct Bayesian priors for the intrinsic rate of increase in the Schaefer model and implications for stock rebuilding. Can. J. Fish. Aquat. Sci. 58: 1871-1890.

Examples

Fdem(1, DLMtool::SimulatedData, plot=TRUE)
#> TAC (median) 
#>     1574.843 
Fdem_CC(1, DLMtool::SimulatedData, plot=TRUE)
#> TAC (median) 
#>     3740.437 
Fdem_ML(1, DLMtool::SimulatedData, plot=TRUE)
#> TAC (median) 
#>     407.0736