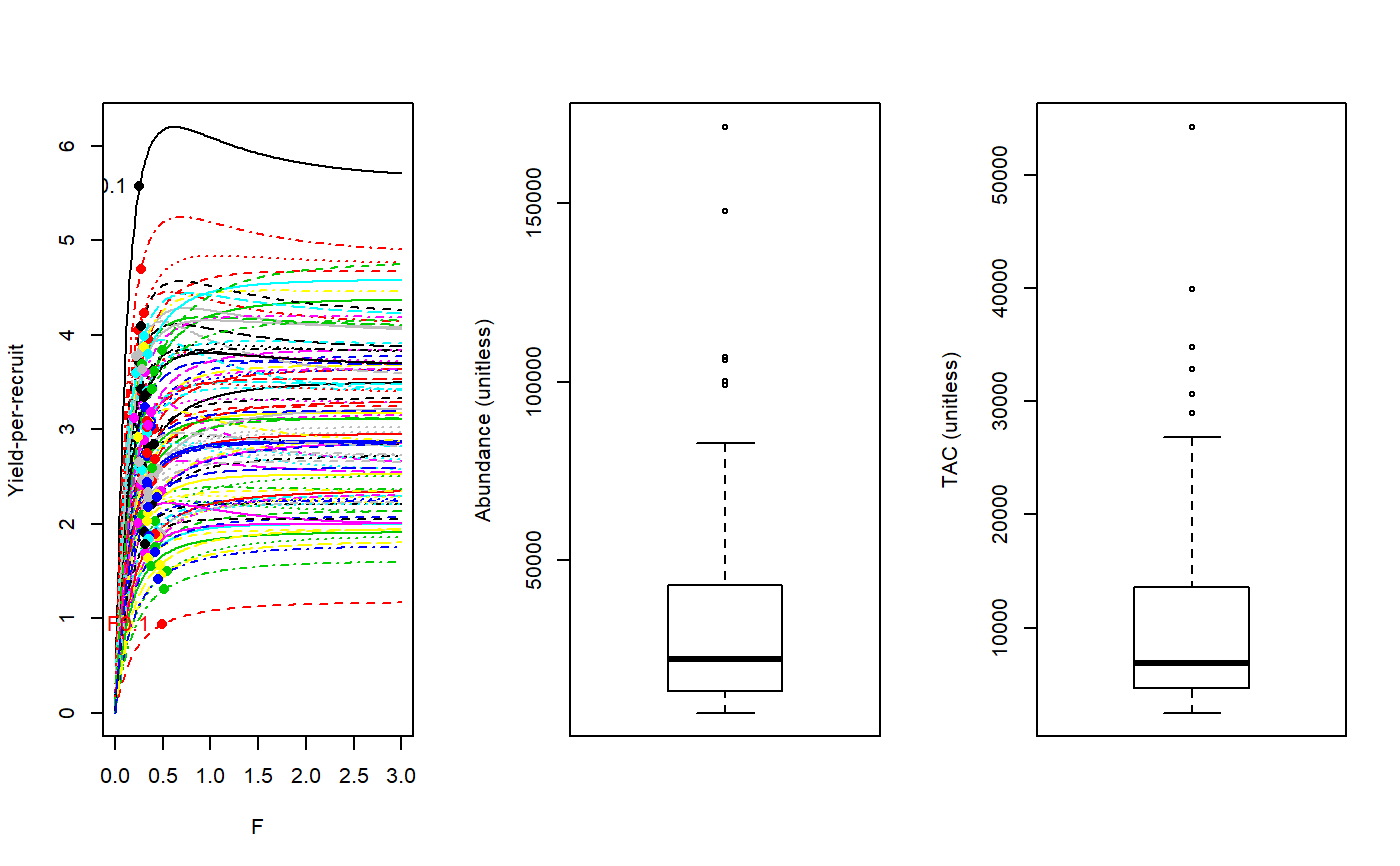
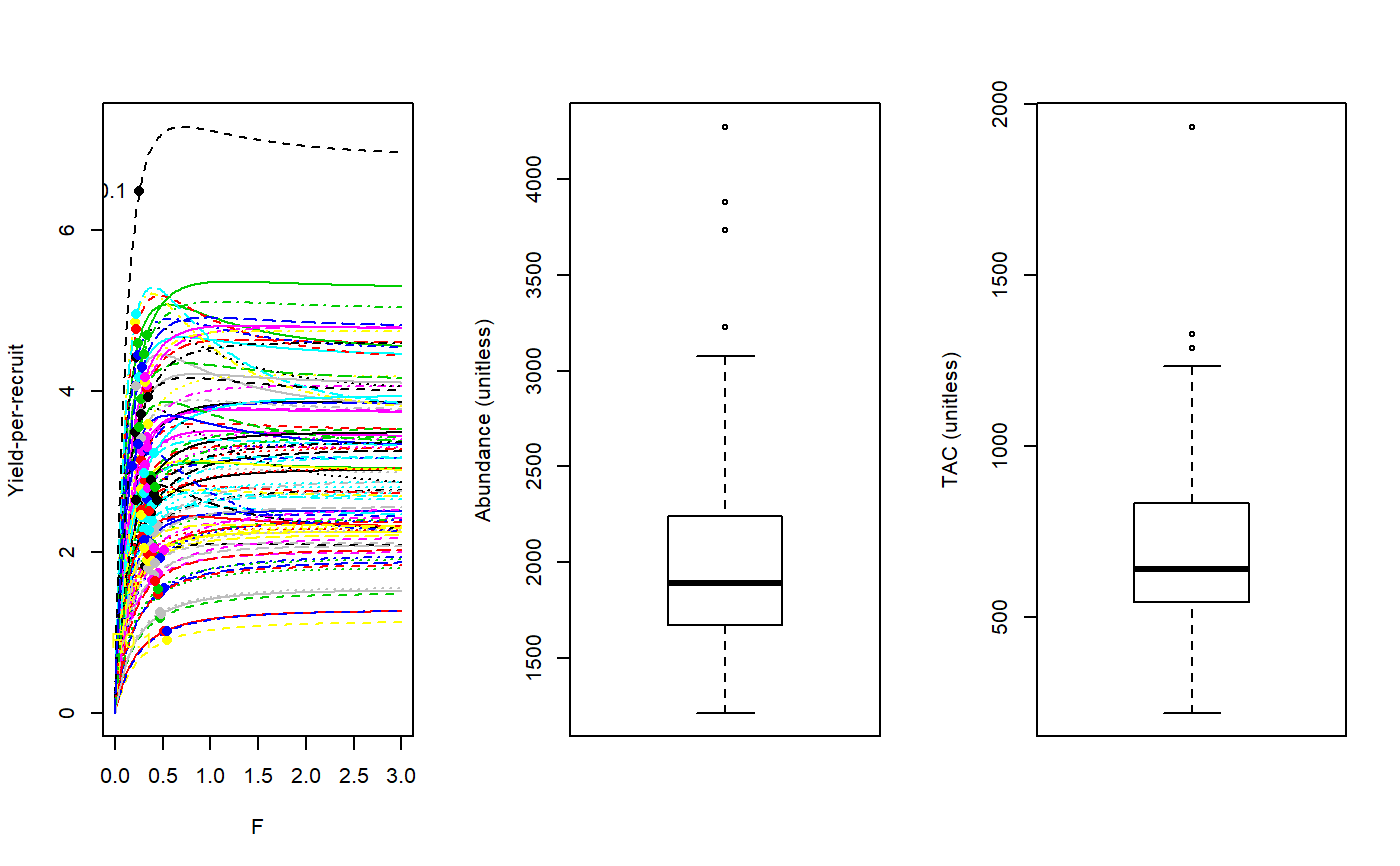
Yield Per Recruit analysis to get FMSY proxy F01

A simple yield per recruit approximation to FMSY (F01) which is the position of the ascending YPR curve for which dYPR/dF = 0.1(dYPR/d0)

YPR(x, Data, reps = 100, plot = FALSE)

YPR_CC(x, Data, reps = 100, plot = FALSE, Fmin = 0.005)

YPR_ML(x, Data, reps = 100, plot = FALSE)

Arguments

x

A position in the data object
Data

A data object
reps

The number of stochastic samples of the MP recommendation(s)
plot

Logical. Show the plot?
Fmin

The minimum fishing mortality rate inferred from the catch-curve analysis

Value

An object of class Rec with the TAC slot populated with a numeric vector of length reps

Details

The TAC is calculated as: $$\textrm{TAC} = F_{0.1} A$$ where \(F_{0.1}\) is the fishing mortality (F) where the slope of the yield-per-recruit (YPR) curve is 10\

The YPR curve is calculated using an equilibrium age-structured model with life-history and selectivity parameters sampled from the Data object.

The variants of the YPR MP differ in the method to estimate current abundance (see Functions section below). #'

Functions

  • YPR: Requires an external estimate of abundance.

  • YPR_CC: A catch-curve analysis is used to determine recent Z which given M (Mort) gives F and thus abundance = Ct/(1-exp(-F))

  • YPR_ML: A mean-length estimate of recent Z is used to infer current abundance.

Note

Based on the code of Meaghan Bryan

Required Data

See Data for information on the Data object

YPR: Abun, LFS, MaxAge, vbK, vbLinf, vbt0

YPR_CC: CAA, Cat, LFS, MaxAge, vbK, vbLinf, vbt0

YPR_ML: CAL, Cat, Lbar, Lc, LFS, MaxAge, Mort, vbK, vbLinf, vbt0

Rendered Equations

See Online Documentation for correctly rendered equations

References

Beverton and Holt. 1954.

Examples

YPR(1, DLMtool::SimulatedData, plot=TRUE)
#> TAC (median) 
#>     2486.766 
YPR_CC(1, DLMtool::SimulatedData, plot=TRUE)
#> TAC (median) 
#>     6908.574 
YPR_ML(1, DLMtool::SimulatedData, plot=TRUE)
#> TAC (median) 
#>     639.3885