Slope in surplus production MP

A management procedure that makes incremental adjustments to TAC recommendations based on the apparent trend in recent surplus production. Based on the theory of Mark Maunder (IATTC)

SPslope(
  x,
  Data,
  reps = 100,
  plot = FALSE,
  yrsmth = 4,
  alp = c(0.9, 1.1),
  bet = c(1.5, 0.9)
)

Arguments

x	A position in the data object
Data	A data object
reps	The number of stochastic samples of the MP recommendation(s)
plot	Logical. Show the plot?
yrsmth	Years over which to smooth recent estimates of surplus production
alp	Condition for modifying the Data (bounds on change in abundance)
bet	Limits for how much the Data can change among years

Value

An object of class Rec with the TAC slot populated with a numeric vector of length reps

Details

Note that this isn't exactly what Mark has previously suggested and is stochastic in this implementation.

The TAC is calculated as: $$\textrm{TAC}_y = \left\{\begin{array}{ll} M \bar{C} & \textrm{if } r < \alpha_1 \\ \bar{C} & \textrm{if } \alpha_1 < r < \alpha_2 \\ \textrm{bet}_2 \textrm{SP} & \textrm{if } r > \alpha_2 \\ \end{array}\right. $$ where $r$ is the ratio of predicted biomass in next year to biomass in current year $\bar{C}$ is the mean catch over the last yrmsth years, $\alpha_1$ and $\alpha_2$ are specified in alp, $\textrm{bet}_1$ and $\textrm{bet}_2$ are specified in bet, $\textrm{SP}$ is estimated surplus production in most recent year, and: $$M = 1-\textrm{bet}_1 \frac{B_y - \tilde{B}_y}{B_y}$$ where $B_y$ is the most recent estimate of biomass and $\tilde{B}$ is the predicted biomass in the next year.

Required Data

See Data for information on the Data object

SPslope: Abun, Cat, Ind, Year

Rendered Equations

See Online Documentation for correctly rendered equations

References

http://www.iattc.org/Meetings/Meetings2014/MAYSAC/PDFs/SAC-05-10b-Management-Strategy-Evaluation.pdf

Examples

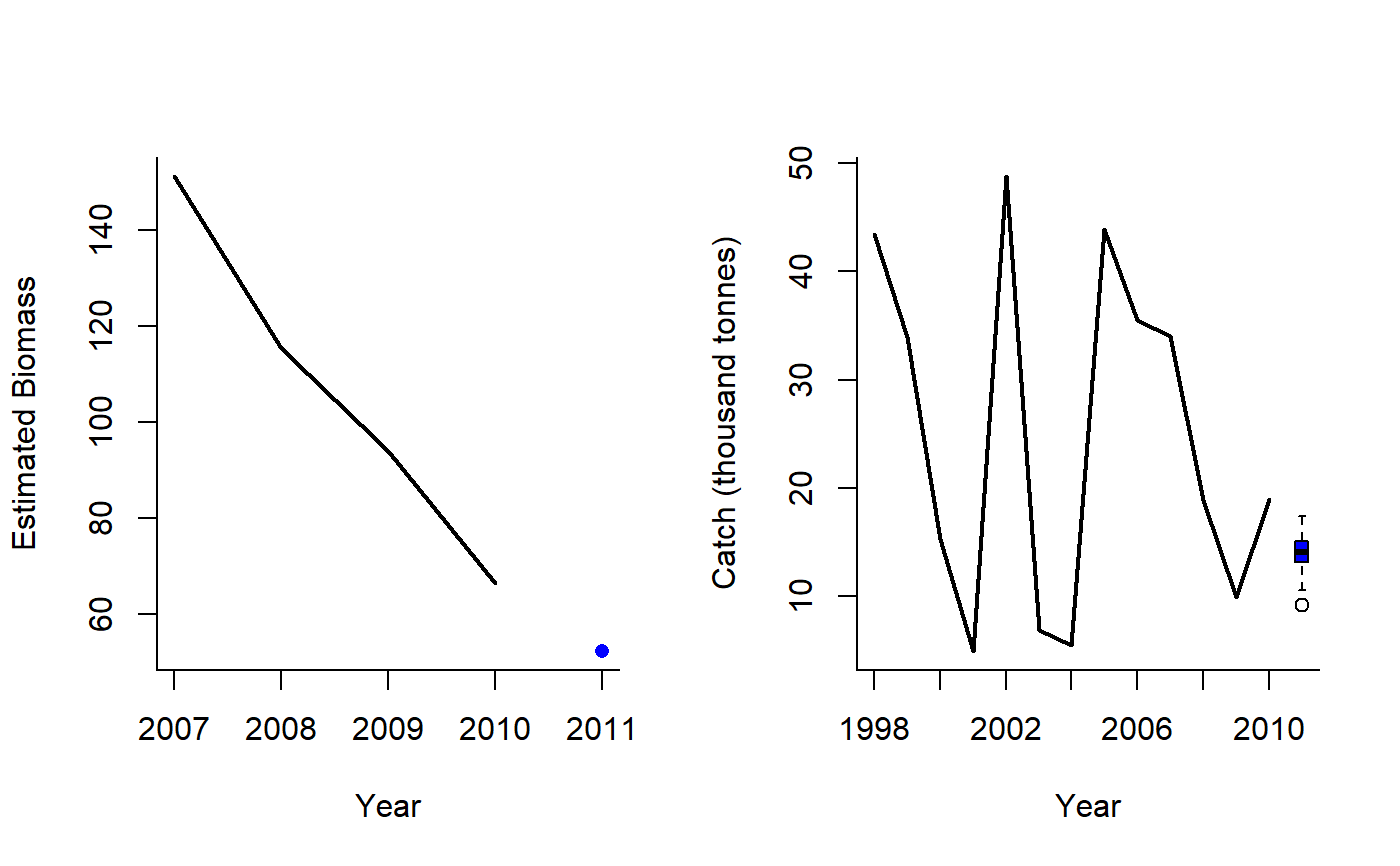
SPslope(1, Data=DLMtool::Atlantic_mackerel, plot=TRUE)
#> TAC (median) 
#>       14.063