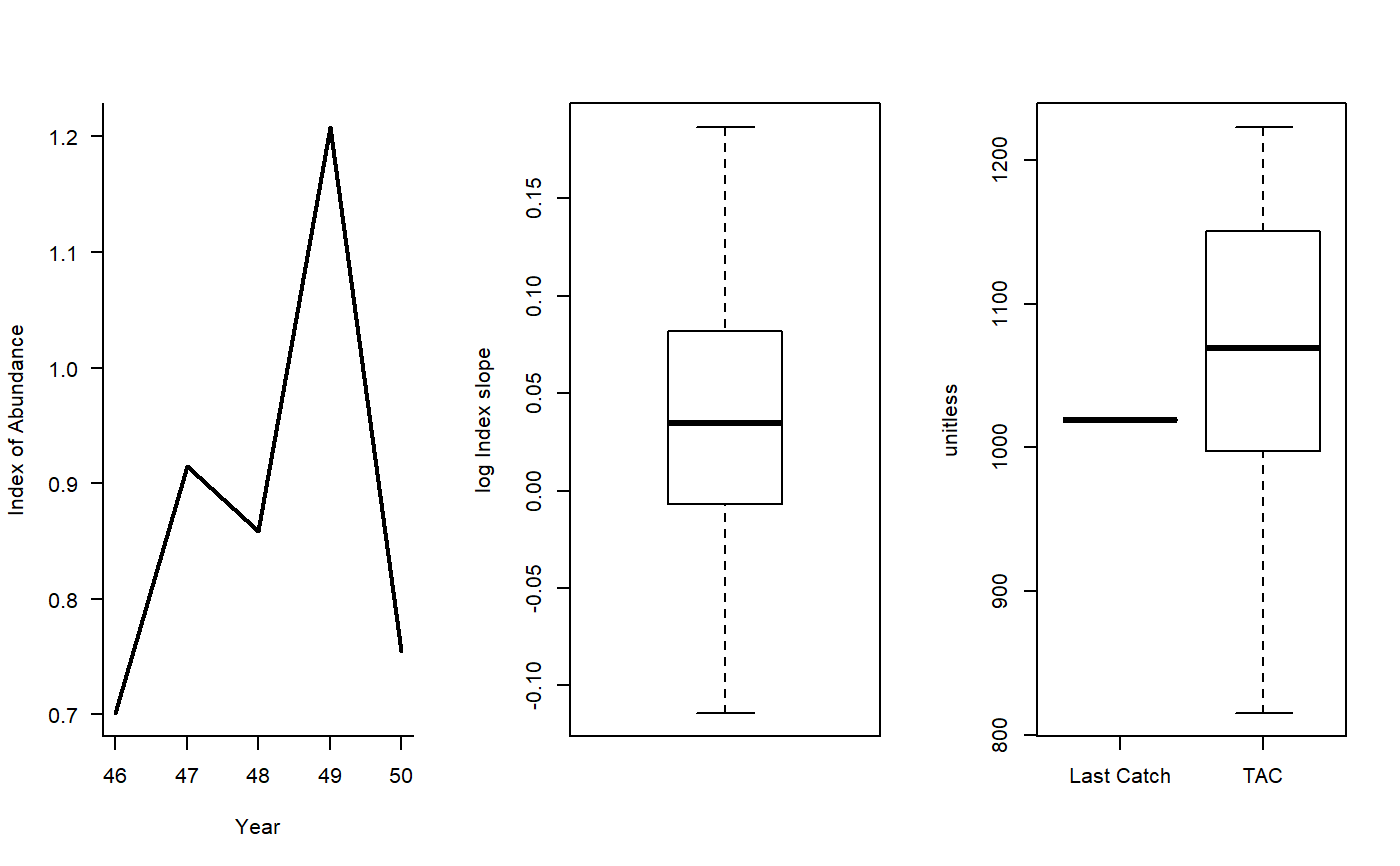
Geromont and Butterworth index slope Harvest Control Rule

An MP similar to SBT1 that modifies a time-series of catch recommendations and aims for a stable catch rates.

GB_slope(x, Data, reps = 100, plot = FALSE, yrsmth = 5, lambda = 1)

Arguments

x

A position in the data object
Data

A data object
reps

The number of stochastic samples of the MP recommendation(s)
plot

Logical. Show the plot?
yrsmth

Number of years for evaluating slope in relative abundance index
lambda

A gain parameter

Value

An object of class Rec with the TAC slot populated with a numeric vector of length reps

Details

The TAC is calculated as: $$\textrm{TAC}_y= C_{y-1} \left(1+\lambda I\right)$$ where \(C_{y-1}\) is catch from the previous year, \(\lambda\) is a gain parameter, and \(I\) is the slope of the linear regression of log Index (Data@Ind) over the last yrsmth years.

The TAC is subject to the following conditions:

  1. if next TAC > 1.2 last catch, then TAC = 1.2 last catch

  2. if next TAC < 0.8 last catch, then TAC = 0.8 last catch

Note that this is my interpretation of their approach and is now stochastic. Currently it is generalized and is not 'tuned' to more detailed assessment data which might explain why in some cases it leads to stock declines.

Required Data

See Data for information on the Data object

GB_slope: Cat, Ind, Year

Rendered Equations

See Online Documentation for correctly rendered equations

References

Geromont, H.F. and Butterworth, D.S. 2014. Complex assessment or simple management procedures for efficient fisheries management: a comparative study. ICES J. Mar. Sci. doi:10.1093/icesjms/fsu017

See also

Other Index methods: GB_target(), Gcontrol(), ICI(), Iratio(), Islope1(), Itarget1_MPA(), Itarget1(), ItargetE1()

Examples

GB_slope(1, DLMtool::SimulatedData, plot=TRUE)
#> TAC (median) 
#>     1069.463