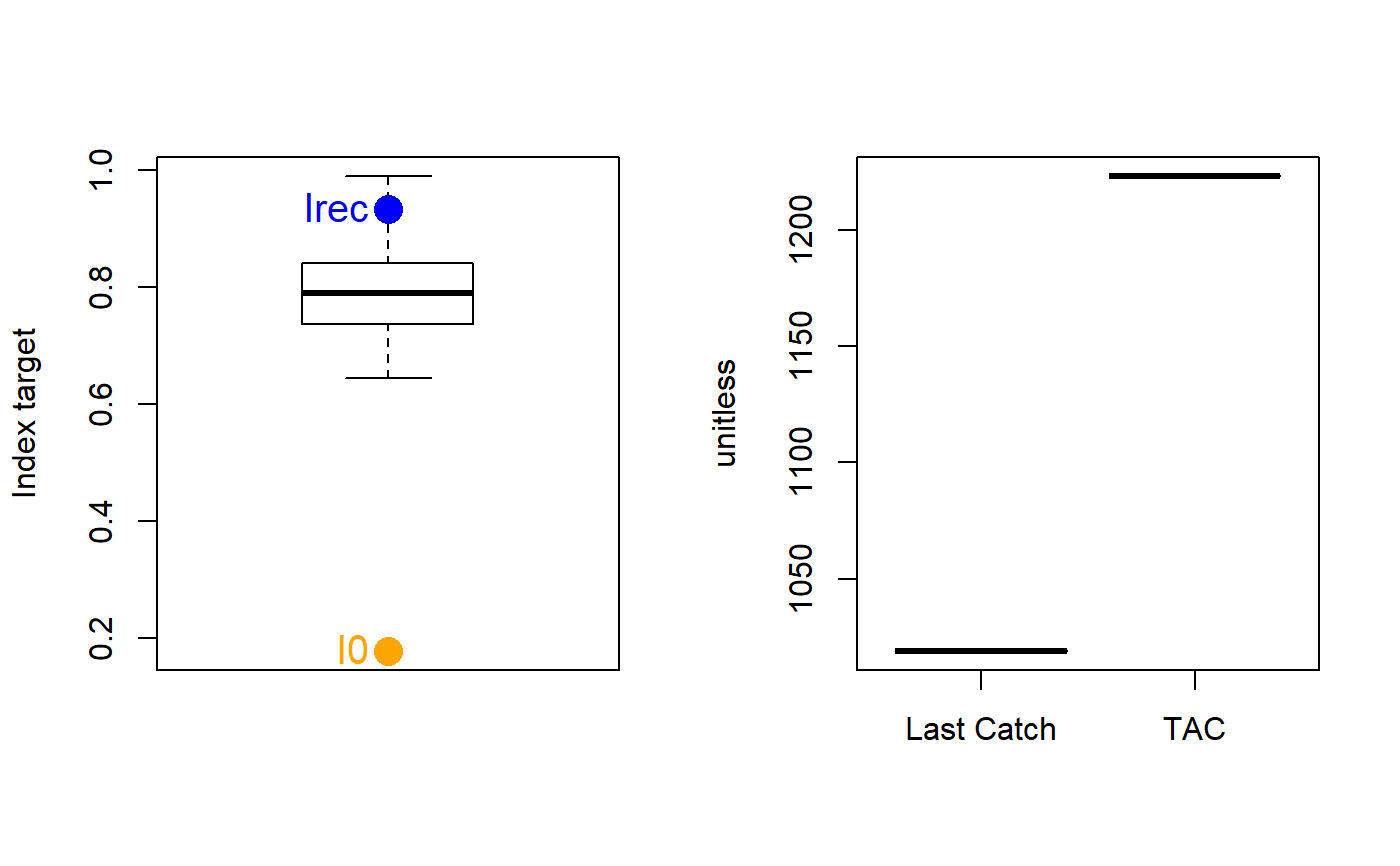Geromont and Butterworth target CPUE and catch MP

An MP similar to SBT2 that modifies a time-series of catch recommendations and aims for target catch rate and catch level based on BMSY/B0 and MSY, respectively.

GB_target(x, Data, reps = 100, plot = FALSE, w = 0.5)

Arguments

x	A position in the data object
Data	A data object
reps	The number of stochastic samples of the MP recommendation(s)
plot	Logical. Show the plot?
w	A gain parameter

Value

An object of class Rec with the TAC slot populated with a numeric vector of length reps

Details

The TAC is calculated as: If $I_\textrm{recent} \geq I_0$: $$\textrm{TAC}= C_\textrm{ref} \left(w + (1-w)\frac{I_\textrm{rec}-I_0}{I_\textrm{target}-I_0} \right) $$

else: $$\textrm{TAC}= wC_\textrm{ref} \frac{I_\textrm{rec}}{I_0}^2$$

where $C_\textrm{ref}$ is a reference catch assumed to be a proxy for MSY (Data@Cref), w is a gain parameter, $I_\textrm{rec}$ is the average index over the last 4 years, $I_\textrm{target}$ is the target Index (Data@Iref), and $I_0$ is 0.2 x the average index over the past 5 years.

In the MSE $C_\textrm{ref}$ is the calculated MSY subject to observation error defined in Obs@CV_Cref, and $I_\textrm{target}$ is assumed to be the index at MSY subject to observation error (Obs@CV_Iref). Consequently, the performance of this method in the MSE is strongly determined by the specified uncertainty for these parameters.

The TAC is subject to the following conditions:

if next TAC > 1.2 last catch, then TAC = 1.2 last catch
if next TAC < 0.8 last catch, then TAC = 0.8 last catch

Required Data

See Data for information on the Data object

GB_target: Cref, Ind, Iref

Rendered Equations

See Online Documentation for correctly rendered equations

References

Geromont, H.F. and Butterworth, D.S. 2014. Complex assessment or simple management procedures for efficient fisheries management: a comparative study. ICES J. Mar. Sci. doi:10.1093/icesjms/fsu017

Examples

 GB_target(1, DLMtool::SimulatedData, plot=TRUE)
#> TAC (median) 
#>     1223.002